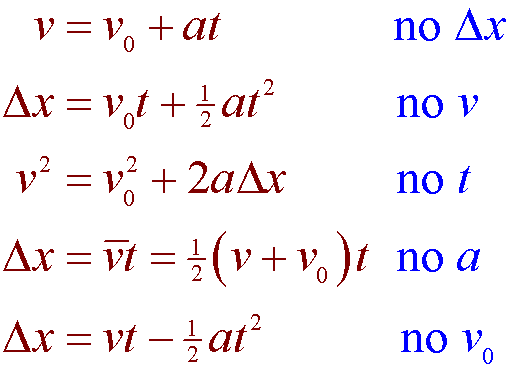Ace Rotational Kinematics Equations

The kinematics of rotational motion describes the relationships among rotation angle angular velocity angular acceleration and time.

Rotational kinematics equations. The rotation Ω will rotate the vector ω changing its direction. The equations are the same as the constant-acceleration equations for 1-D motion substituting the rotational equivalents of the straight-line motion variables. This is a consequence of our earlier observation that in a rigid body rotating with angular velocity ω every point rotates with angular velocity ω.

The second column consists of. To derive rotational equations from the linear counterparts we used the relationships arα vrω and xrθ. These are essentially the one-dimensional motion equations in disguise.

To determine this equation we recall a familiar kinematic equation for translational or straight-line motion. Rotational kinematic equations equations used to solve rotational motion numerical In these equations the subscript 0 denotes initial values ω0 and vo are initial values. By using the relationships between velocity and angular velocity distance and angle of rotation and acceleration and angular acceleration rotational kinematic equations can be derived from their linear motion counterparts.

0 d dt t0 t t0 1 2 d2 dt2 t0. Rotation with constant angular acceleration constant angular acceleration meaningif angular acceleration is constant then the angular velocity must beconsta. The 4 equations in the first column represent the rotational kinematics.

Rotational kinematics For motion with constant angular acceleration α ωf - ωi t f - t i Δ ω Δt we have Δ ω ω Δt ωf ωi α Δt. Kinematics is the description of motion. Equations for Rotational Kinematics Since velocity is change in position divided by time angular velocity is change in angle divided by time.

Let us start by finding an equation relating ω α ω α and t. It explains how to solve rotational kinematic problems using a few sim. 25 rows If motion gets equations then rotational motion gets equations too.